Nuestro malabarista de la semana pasada no tomó la mejor decisión al pasar por un puente tan precario lanzando al aire sus bolos, pues su reacción al lanzarlos verticalmente hacia arriba —así como su impacto al volver a las manos del artista circense— ejerce sobre el puente una fuerza mayor que su peso en reposo. Ni siquiera un malabarista puede saltarse la tercera ley de Newton.
Algunos lectores han sugerido usar una báscula para comprobar lo anterior y para cuantificar el efecto. Si tienes en casa el típico “pesapersonas” para controlar los efectos de la dieta (y un techo lo suficientemente alto), puedes intentar —bajo tu responsabilidad— el siguiente experimento: coge un objeto de un kilo o más (un brik de cualquier líquido, por ejemplo), súbete a la báscula con él en las manos y lánzalo ligeramente hacia arriba sin perder de vista el marcador de la báscula; comprobarás que en el momento del lanzamiento y en el de la recuperación del objeto (si logras recuperarlo al vuelo) la aguja se desplaza ligeramente hacia la derecha.
El problema del malabarista recuerda uno que se planteó, hace muchos años, en un examen de física de una escuela de ingeniería y que, en su momento, se hizo famoso:
Sobre una báscula hay una jaula que, estando vacía, pesa un kilo con un pajarito que pesa 30 gramos posado en su balancín. De pronto el pájaro empieza a revolotear por el interior de la jaula, ¿cuánto marca la aguja de la báscula?
Una variación sobre el mismo tema:
Ahora es una pequeña pecera con un pez la que está sobre la báscula. La pecera y el agua pesan un kilo y el pez 30 gramos. De pronto el pez salta fuera del agua y vuelve a caer en la pecera, ¿cómo repercute este salto en la aguja de la báscula?
Y una variación sobre la variación:
En la pecera de antes, con la misma cantidad de agua, no hay un pez sino una bola de hierro que pesa un kilo descansando en el fondo. Si metes la mano en la pecera y sacas la bola de hierro, ¿qué marca la aguja de la báscula en los distintos momentos de esta acción?
La equivalencia del sobre y los puentes
Y de un problema sobre un puente (en ambos sentidos de la preposición) a otro de sobres y puentes paralelos:
El famoso recorrido por los 7 puentes de Königsberg no era posible porque a las cuatro partes de la ciudad le correspondían un número impar de puentes: 5 a una de las islas, 3 a la otra, 3 a la margen derecha del río y 3 a la izquierda (suman 14, sí, pero es que cada puente lo hemos contado dos veces). Por lo tanto, partieras de donde partieras, si recorrías todos los puentes sin volver a pasar por ninguno, tenías que hacer algo imposible para cumplir la tarea: acabar el recorrido en las otras tres partes a la vez (puesto que todas ellas las visitas según la secuencia entrar-salir-entrar, o entrar-salir-entrar-salir-entrar en el caso de la isla con 5 puentes). Para que el recorrido euleriano fuera posible empezando en una zona y terminando en otra (como ocurre en la actual Kaliningrado), tendría que haber dos zonas con un número par de puentes y dos con un número impar.

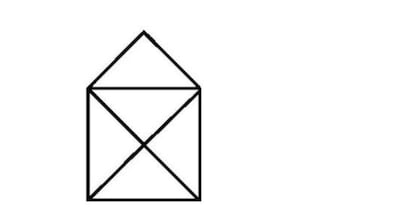
Al pasar de Königsberg a Kaliningrado y de 7 puentes a 5, hay 21 parejas de puentes distintas que podrían haber desaparecido (7×6/2). Y 15 de estas parejas, al desaparecer, dejan dos zonas con un número par de puentes y las otras dos con un número impar. Por ejemplo, si eliminamos los puentes marcados en la figura (que a primera vista parecen los más prescindibles), ambas islas quedan con 3 puentes y ambas orillas con 2. Por lo tanto, necesitamos algún dato adicional para saber cuál de las 15 parejas de puentes posibles ha sido eliminada. Lo que podemos afirmar es que, sean cuales fueren los puentes desaparecidos, ahora el problema -resoluble- de los puentes de Kaliningrado es equivalente al archiconocido de dibujar un sobre abierto sin levantar el lápiz del papel ni pasar dos veces por el mismo trazo. ¿Ves la equivalencia? Y no digas que las zonas de Kaliningrado son 4 mientras que el sobre tiene 5 vértices (¿por qué no has de decirlo?).
Y puesto que llevamos un par de semanas hablando de grafos, aunque sin apenas nombrarlos, aprovecho para recomendar una vez más el estupendo y divertido libro de Clara Grima En busca del grafo perdido. Como dije en su día, al empezar a leerlo pensé: “¿Por qué no lo habré escrito yo?”, pero al acabarlo me dije: “Es mejor que lo haya escrito ella”.
Puedes seguir a MATERIA en Facebook, X e Instagram, o apuntarte aquí para recibir nuestra newsletter semanal.
Suscríbete para seguir leyendo
Lee sin límites
_
